Решите следующий числовой ребус — пример на деление без остатка, в котором все цифры заменены буквами:
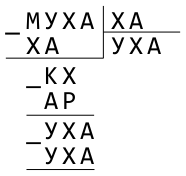
Примечание: Здесь цифры заменены буквами, причём одинаковыми буквами заменены одинаковые цифры, а разными буквами — неодинаковые цифры.
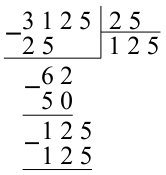
Рассуждения, приводящие к этому ответу, могут быть примерно следующими.
- Прежде всего, поскольку при умножении У на ХА получается снова ХА, то
У = 1 . - При умножении Х на ХА получается двузначное число. Следовательно,
Х = 2 илиХ = 3 (Х не может равняться 1, поскольку эта цифра уже занята буквой У, а для цифр, больших 3, произведение ХА на Х будет уже трёхзначным).- Если предположить, что
Х = 3 , тоА = 2 (А не может равняться 2 или 3, потому что эти цифры уже заняты, а для больших цифр произведение ХА на Х будет трехзначным). Но такого не может быть, поскольку тогда произведение ХА на А (равное УХА) не будет трехзначным. - Следовательно,
Х = 2 .
- Если предположить, что
- Если
Х = 2 , то произведение ХА на Х может начинаться только на 4 или на 5, то есть либоА = 4 , либоА = 5 .- Если
А = 4 , то произведение ХА на А (равное УХА) не будет трёхзначным. - Следовательно,
А = 5 .
- Если
- Теперь, имея на руках делитель и частное, совсем легко получить значения остальных цифр:
М = 3 ,К = 6 ,Р = 0 .
