Пять булыжников

Обозначим булыжники буквами от «А» до «Д» и будем для наглядности процесс взвешиваний представлять в графическом виде (в виде ориентированного графа):

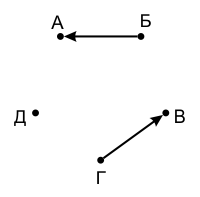
Этот рисунок — граф — говорит о том, что было произведено 2 взвешивания: сравнивались булыжники А и Б, а также В и Г, причём булыжник Б оказался тяжелее А, а булыжник Г оказался тяжелее В.

Если первый булыжник тяжелее второго, а второй тяжелее третьего, то можно сделать вывод, что первый булыжник тяжелее третьего (это называется транзитивностью). Такие «выводы» мы будем обозначать на графе серыми стрелками:

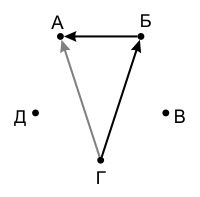
Этот граф говорит о том, что было произведено 2 взвешивания: сравнивались булыжники А, Б и Б, Г, причём оказалось, что А < Б < Г. Отсюда мы делаем вывод, что А < Г, что и обозначено серой стрелкой.

В графе с пятью точками (вершинами) можно провести максимум 10 стрелок (рёбер). Решить задачу — это значит провести все 10 стрелок, то есть для каждой пары булыжников указать, какой из них тяжелее. Очевидно, что из этих 10 стрелок 7 или меньше будут чёрного цвета (явные взвешивания) и 3 или больше — серого (неявные выводы).
Значит, если в процессе решения мы получим на графе 3 или больше серых ребра (даже если всего стрелок будет ещё меньше 10), то задачу можно считать решённой, поскольку для недостающих рёбер у нас в запасе будет достаточное количество взвешиваний.

После этого длинного вступления наконец перейдём к алгоритму решения головоломки.

• Первыми тремя взвешиваниями сравним булыжники А и Б, Г и В, а также те два булыжника, которые каждый в своей паре оказались тяжелее. Можно считать, что A < Б, В < Г и Б < Г (если это не так, то просто переименуем булыжники нужным образом):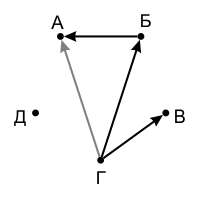
  

  

  (Сразу проводим и соответствующую серую стрелку.)

• Четвёртым взвешиванием сравниваем Д и Б. Возможны 2 варианта:
  • Д > Б:
    

    

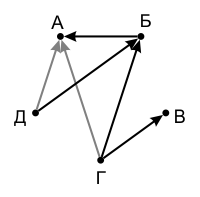
    В этому случае пятым взвешиванием сравниваем Б и В. Независимо от результата этого сравнения мы получаем 3 серых стрелки и поэтому считаем алгоритм завершённым:

    

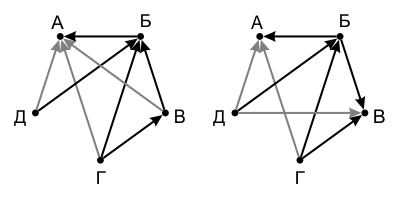
  • Д < Б:
    

    

    В этому случае пятым взвешиванием сравниваем А и Д (это не приносит нам дополнительных серых стрелок), а шестым — В и тот из булыжников А или Д, который оказался тяжелее другого. Например, если А < Д (случай Д < А симметричен и рассматривается аналогично), то после шестого взвешивания мы имеем один из двух вариантов, каждый из которых содержит по 3 серых стрелки и требует лишь одного — заключительного — взвешивания: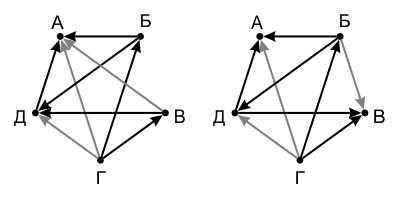

    

    Таким образом, и эта ветка алгоритма завершается нашей безоговорочной победой.